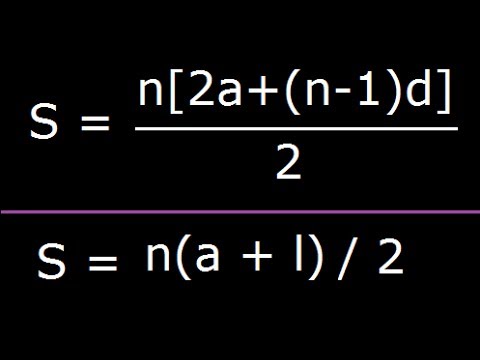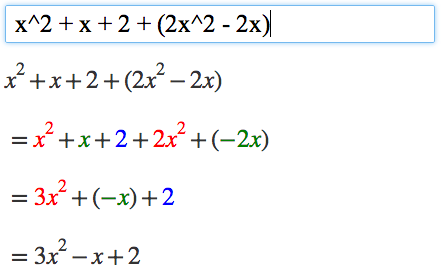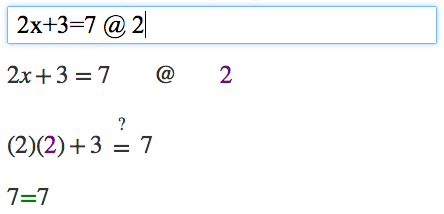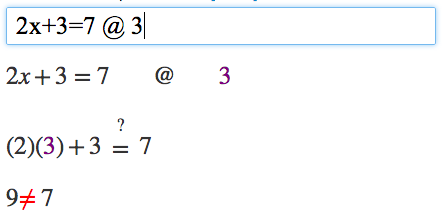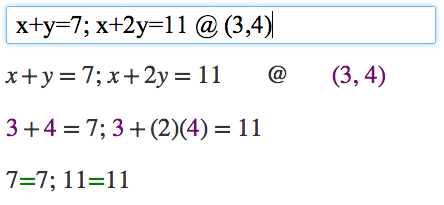Tuesday, 12 July 2016
Inequalities
| 1) | 
Graphically, the solution is:
| The only difference between the linear equation "x + 3 = 2" and this linear inequality is that I have a "less than" sign, instead of an "equals" sign. The solution method is exactly the same: subtract 3 from either side.Note that the solution to a "less than, but not equal to" inequality is graphed with a parentheses (or else an open dot) at the endpoint, indicating that the endpoint is not included within the solution. |
| 2) | 
Graphically, the solution is:
| The only difference between the linear equation "2 – x = 0" and this linear inequality is the "greater than" sign in place of an "equals" sign.Note that "x" in the solution does not "have" to be on the left. However, it is often easier to picture what the solution means with the variable on the left. Don't be afraid to rearrange things to suit your taste. |
| 3) | 
Graphically, the solution is:
| The only difference between the linear equation "4x + 6 = 3x – 5" and this inequality is the "less than or equal to" sign in place of a plain "equals" sign. The solution method is exactly the same.Note that the solution to a "less than or equal to" inequality is graphed with a square bracket (or else a closed dot) at the endpoint, indicating that the endpoint is included within the solution. |
| 4) |
Graphically, the solution is:
| The solution method here is to divide both sides by a positive two. Copyright © Elizabeth Stapel 1999-2011 All Rights Reserved |
| 5) | 
Graphically, the solution is:
| This is the special case noted above. When I divided by the negative two, I had to flip the inequality sign. |
http://www.purplemath.com/modules/ineqsolv.htm
this video will help u to understand more about the inequalities..

Arithmetic progression
Mean median mode
The only way to master maths is to do lots of maths practice...
easy way to learn Mean/Median/mode
https://www.youtube.com/watch?v=k3aKKasOmIw

algebra
Let's solve your equation step-by-step.
3 x + 2 = 14 3 x + 2 − 2 = 14 − 2 3 x = 12
3 x 3
=
12 3
x = 4
Answer:
x = 4
MATH SYMBOLS
If you would like to create your own math expressions, here are some symbols that Algebra Calculator understands:
+ (Addition)
- (Subtraction)
* (Multiplication)
/ (Division)
^ (Exponent: "raised to the power")
- (Subtraction)
* (Multiplication)
/ (Division)
^ (Exponent: "raised to the power")
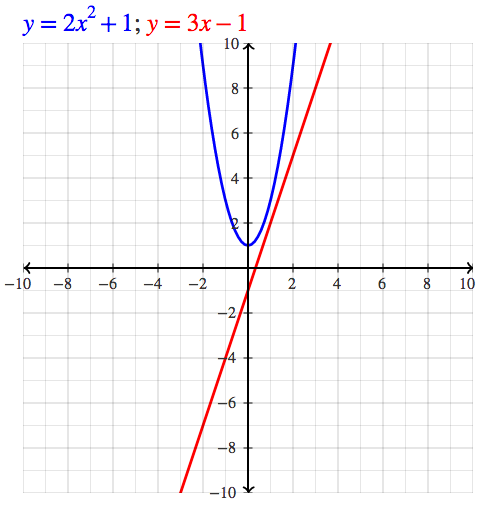
GRAPHING
To graph an equation, enter an equation that starts with "y=" or "x=". Here are some examples: y=2x^2+1, y=3x-1, x=5, x=y^2.
To graph a point, enter an ordered pair with the x-coordinate and y-coordinate separated by a comma, e.g., (3,4).
To graph two objects, simply place a semicolon between the two commands, e.g., y=2x^2+1; y=3x-1.
POLYNOMIALS
Algebra Calculator can simplify polynomials, but it only supports polynomials containing the variable x.
Here are some examples: x^2 + x + 2 + (2x^2 - 2x), (x+3)^2.
EVALUATING EXPRESSIONS
Algebra Calculator can evaluate expressions that contain the variable x.
To evaluate an expression containing x, enter the expression you want to evaluate, followed by the @ sign and the value you want to plug in for x. For example the command 2x @ 3 evaluates the expression 2x for x=3, which is equal to 2*3 or 6.
Algebra Calculator can also evaluate expressions that contain variables x and y. To evaluate an expression containing x and y, enter the expression you want to evaluate, followed by the @ sign and an ordered pair containing your x-value and y-value. Here is an example evaluating the expression xy at the point (3,4): xy @ (3,4).
CHECKING ANSWERS FOR SOLVING EQUATIONS
Just as Algebra Calculator can be used to evaluate expressions, Algebra Calculator can also be used to check answers for solving equations containing x.
As an example, suppose we solved 2x+3=7 and got x=2. If we want to plug 2 back into the original equation to check our work, we can do so: 2x+3=7 @ 2. Since the answer is right, Algebra Calculator shows a green equals sign.
If we instead try a value that doesn't work, say x=3 (try 2x+3=7 @ 3), Algebra Calculator shows a red "not equals" sign instead.
To check an answer to a system of equations containing x and y, enter the two equations separated by a semicolon, followed by the @ sign and an ordered pair containing your x-value and y-value. Example: x+y=7; x+2y=11 @ (3,4).
Subscribe to:
Comments (Atom)