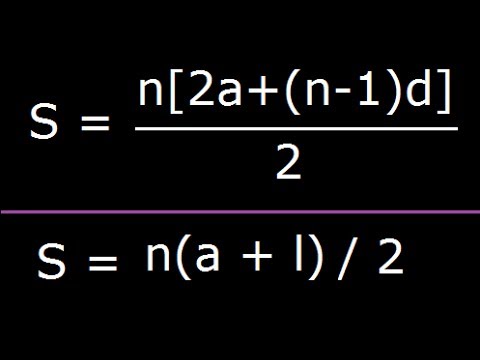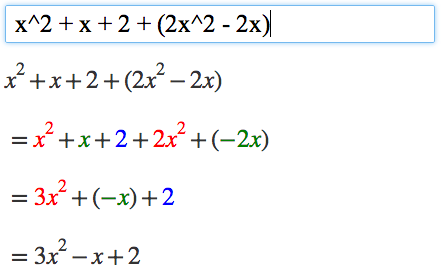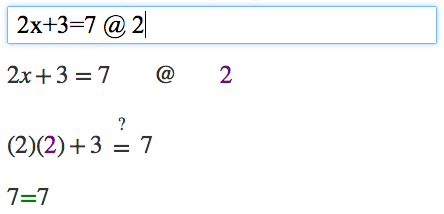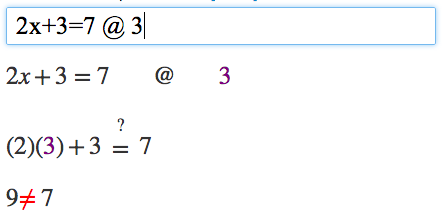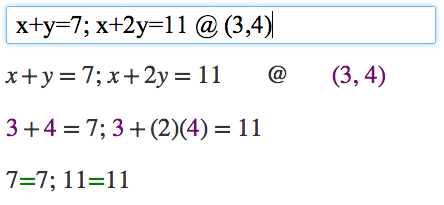Tuesday, 12 July 2016
Inequalities
| 1) | 
Graphically, the solution is:
| The only difference between the linear equation "x + 3 = 2" and this linear inequality is that I have a "less than" sign, instead of an "equals" sign. The solution method is exactly the same: subtract 3 from either side.Note that the solution to a "less than, but not equal to" inequality is graphed with a parentheses (or else an open dot) at the endpoint, indicating that the endpoint is not included within the solution. |
| 2) | 
Graphically, the solution is:
| The only difference between the linear equation "2 – x = 0" and this linear inequality is the "greater than" sign in place of an "equals" sign.Note that "x" in the solution does not "have" to be on the left. However, it is often easier to picture what the solution means with the variable on the left. Don't be afraid to rearrange things to suit your taste. |
| 3) | 
Graphically, the solution is:
| The only difference between the linear equation "4x + 6 = 3x – 5" and this inequality is the "less than or equal to" sign in place of a plain "equals" sign. The solution method is exactly the same.Note that the solution to a "less than or equal to" inequality is graphed with a square bracket (or else a closed dot) at the endpoint, indicating that the endpoint is included within the solution. |
| 4) |
Graphically, the solution is:
| The solution method here is to divide both sides by a positive two. Copyright © Elizabeth Stapel 1999-2011 All Rights Reserved |
| 5) | 
Graphically, the solution is:
| This is the special case noted above. When I divided by the negative two, I had to flip the inequality sign. |
http://www.purplemath.com/modules/ineqsolv.htm
this video will help u to understand more about the inequalities..

Arithmetic progression
Mean median mode
The only way to master maths is to do lots of maths practice...
easy way to learn Mean/Median/mode
https://www.youtube.com/watch?v=k3aKKasOmIw

algebra
Let's solve your equation step-by-step.
3 x + 2 = 14 3 x + 2 − 2 = 14 − 2 3 x = 12
3 x 3
=
12 3
x = 4
Answer:
x = 4
MATH SYMBOLS
If you would like to create your own math expressions, here are some symbols that Algebra Calculator understands:
+ (Addition)
- (Subtraction)
* (Multiplication)
/ (Division)
^ (Exponent: "raised to the power")
- (Subtraction)
* (Multiplication)
/ (Division)
^ (Exponent: "raised to the power")
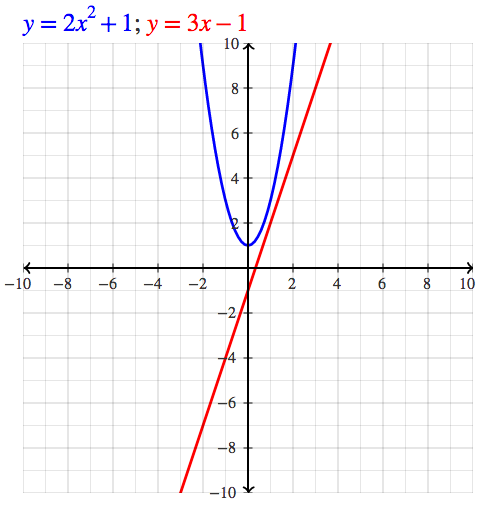
GRAPHING
To graph an equation, enter an equation that starts with "y=" or "x=". Here are some examples: y=2x^2+1, y=3x-1, x=5, x=y^2.
To graph a point, enter an ordered pair with the x-coordinate and y-coordinate separated by a comma, e.g., (3,4).
To graph two objects, simply place a semicolon between the two commands, e.g., y=2x^2+1; y=3x-1.
POLYNOMIALS
Algebra Calculator can simplify polynomials, but it only supports polynomials containing the variable x.
Here are some examples: x^2 + x + 2 + (2x^2 - 2x), (x+3)^2.
EVALUATING EXPRESSIONS
Algebra Calculator can evaluate expressions that contain the variable x.
To evaluate an expression containing x, enter the expression you want to evaluate, followed by the @ sign and the value you want to plug in for x. For example the command 2x @ 3 evaluates the expression 2x for x=3, which is equal to 2*3 or 6.
Algebra Calculator can also evaluate expressions that contain variables x and y. To evaluate an expression containing x and y, enter the expression you want to evaluate, followed by the @ sign and an ordered pair containing your x-value and y-value. Here is an example evaluating the expression xy at the point (3,4): xy @ (3,4).
CHECKING ANSWERS FOR SOLVING EQUATIONS
Just as Algebra Calculator can be used to evaluate expressions, Algebra Calculator can also be used to check answers for solving equations containing x.
As an example, suppose we solved 2x+3=7 and got x=2. If we want to plug 2 back into the original equation to check our work, we can do so: 2x+3=7 @ 2. Since the answer is right, Algebra Calculator shows a green equals sign.
If we instead try a value that doesn't work, say x=3 (try 2x+3=7 @ 3), Algebra Calculator shows a red "not equals" sign instead.
To check an answer to a system of equations containing x and y, enter the two equations separated by a semicolon, followed by the @ sign and an ordered pair containing your x-value and y-value. Example: x+y=7; x+2y=11 @ (3,4).
Wednesday, 8 June 2016
Logarithm
Bases and Exponents
A power function has the forma is known as the base, while x is called the power or exponent, and the power function means that a is multiplied by itself x times:
y(x)
|
=
| ax | ||
=
| a·a·····a | |||
| x times | . |
Example:
y(3)
|
=
|
23
| ||
=
| 2·2·2 | |||
=
| 8 | . |
§1.2 Combinations of Bases and Powers
Some simple combinations of bases and powers illustrate the utility of power functions.§1.2.1 Powers of Products
If the base of a power function is a product of two numbers, (a·b)x, multiplying out and rearranging the terms tells us that the result can be expressed as the the product of two powers:
Explanation:
(a·b)x
|
=
| (a·b·a·b·····a·b) | ||||
x times
| ||||||
| (a·a·····a) | · | (b·b·····b) | ||||
x times
|
x times
| |||||
=
|
ax·bx
| . | ||||
Example:
(2·3)2
|
=
| 22·32 | ||
62
|
=
|
4·9
| ||
36
|
=
|
36
| . |
§1.2.2 Multiplication of Power Functions
When power functions with the same base are multiplied together, aw·ax, that base is multiplied by itself w times, and then again by x times, which is equivalent to adding their exponents:
Explanation:
aw·ax
|
=
| (a·a·····a) | · | (a·a·····a) | ||
w times
|
x times
| |||||
=
|
(a·a·a·a·····a·a)
| |||||
w + x times
| ||||||
=
|
aw+x
| . | ||||
Example:
24·23
|
=
| (2·2·2·2)·(2·2·2) | ||
=
|
27
| . |
§1.2.3 Division of Power Functions
When power functions with the same base are dividing each other, aw/ax, that base is multiplied by itself w times, and then divided by the base multiplied by itself x times, which is equivalent to subtracting their exponents:
Explanation:
aw / ax
|
=
| (a·a·····a) | / | (a·a·····a) | ||
w times
|
x times
| |||||
=
|
(a·a·a·a·····a·a)
| |||||
w – x times
| ||||||
=
|
aw–x
| . | ||||
Example:
24 / 23
|
=
| (2·2·2·2) / (2·2·2) | ||
=
|
21
| . |
§1.2.4 Powers of Powers
If a power function is itself a base of another power, (aw)x, the base a is multiplied by itself w times, and the result is then multiplied together x times, which is equivalent to multiplying their exponents:
Explanation:
(aw)x
|
=
| (a·a·····a) | · | (a·a·····a) | ····· | (a·a·····a) | ||
w times
|
w times
|
w times
| ||||||
x times
| ||||||||
=
|
(a·a·a·a·····a·a)
| |||||||
w · x times
| ||||||||
=
|
aw·x
| . | ||||||
Example:
(24)3
|
=
| (2·2·2·2)·(2·2·2·2)·(2·2·2·2) | ||
=
|
27
| . |
§1.3 Particular Exponent Values
The previous examples have implied that exponents were positive integers. But all types of exponents are possible.§1.3.1 Special Exponents of 0 and 1
One special case is the exponent of 1, which means that the base a is multiplied by itself just one time:Another special case is the exponent of 0, which means that there are no multiplications of the base at all:
Another way to see that a0 is equal to 1 is to divide any power function by itself:
ax/ax
|
=
|
ax–x
| ||
1
|
=
|
a0
| . |
§1.3.2 Negative Exponents
We see from above that decreasing the exponent is equivalent to dividing by the base. Eventually we must reach a number less than one, so it shouldn't be a surprise to understand a negative exponent as being 1 divided by the base raised to the positive exponent:
Explanation:
a–1
|
=
| a0–1 | ||
=
| a0/a1 | Why? | ||
=
| 1/a | Why? | ||
a–x
|
=
| (a–1)x | Why? | |
=
| (1/a)x | |||
=
| 1x/ax | Why?. | ||
=
| 1/ax | Why?. |
Example:
2–3
|
=
| 1/(2·2·2) | ||
=
|
1/8
| . |
§1.3.3 Rational Exponents
Suppose an exponent in a power function y = ax is a non-integer rational value, e.g. a fraction such 2/3.Let's first consider a rational exponent of the form 1/n, y = a1/n; since multiplying it together n times must result in just a, this must be the nth root of a:
Explanation:
(a1/n)n
|
=
| an/n | Why? | |
=
| a1 | |||
=
|
a
| Why?. |
Example:
(41/2)2
|
=
| 41 | ||
(±2)2
|
=
|
4
| . |
So, any base a raised to a rational exponent can be expressed as an nth root of a raised to an integer power.
)m
Example:
163/4
|
=
| (161/4)3 | ||
=
| (±2)3 or (±2 i)3 | |||
=
| ±8 or ±8 i | . |
§1.3.4 Real Exponents
If the exponent in a power function y = ax is an integer, y can be calculated in a straightforward fashion:
y(2)
|
=
|
42
| ||
=
| 4·4 | |||
=
| 16 | ; | ||
y(3)
|
=
|
43
| ||
=
| 4·4·4 | |||
=
| 64 | . |
y(2.5)
|
=
| 42.5 | ||
=
| 42+1/2 | |||
=
| 42 · 41/2 | Why? | ||
=
| 16 · ±2 | Why? | ||
=
| ±32 | . |
y(2.56789)
|
=
| 4.12.56789 | ||
=
| 37.459... |
Note that, while roots can be negative or complex, a scientific calculator will only return a real and preferably positive root (though that's generally what you want).
Scientific calculators are able to calculate these functions by approximating them with a sum of rational values.
§1.4 Particular Base Values
Some values of the base of a power function have particular use and importance.§1.4.1 Special Base 1
The base 1 is special because it is unaffected by any exponent, since multiplying by 1 never changes a value:
Explanation:
1x
|
=
| 1·1·····1 | ||
| x times | ||||
=
| 1 | . |
§1.4.2 Base 10 and Scientific Notation
Because our number system is based on the number 10, it is often convenient to express very large and very small numbers as a value w between 1 and 10 (the prefactor) multiplied by a power of 10:
Examples:
37.46
|
=
|
3.746 · 101
| ||
1249
|
=
|
1.249 · 103
| ||
521,700
|
=
|
5.217 · 105
| ||
0.02836
|
=
|
2.836 · 10–2
| . |
Scientific calculators have a special key to enter the base-10 exponent after the prefactor, often labeled EXP or EE (for "Enter Exponent").
When displaying such numbers, calculators and computer programming languages will often drop the "· 10", writing them in a format such as "5.21705" or " 5.217e05".
§1.4.3 The Base e and the Exponential Function
One particular base is of singular importance in math and science: the transcendental numberThe base e shows up naturally in calculus because the power of this base is equal to its own derivative:
y
|
=
| ex | ||
| dy/dx |
=
| ex | . |
ex
|
=
| exp(x) | . |
For reasons we'll see later, any power function can be expressed as a power of the exponential function:
ax
|
=
| ex/l | , |
l
|
=
| 1 / ln a | . |
The scale l describes the amount of change in x required for a change in the function by a factor of e, which is a common standard of comparison.
§1.4.4 Negative Bases
Negative bases can always be separated into factors of -1 and a positive base:Unless the exponent x is an integer, the factor (–1)x will likely be a complex number, e.g.
(–1)1/2
|
=
| i | . |
§1.5 Graphs of Power Functions
Since we have defined power functions for all real exponents, we can draw graphs of them to see how they behave in general:
Note the special base a = 1, as well as the function values at the special exponents x = 0 and 1.
Note also the left-right symmetry of 2x and 2–x.
This graph should help you understand why the term "exponential" is so commonly used to describe a rapid change, either an increase or a decrease.
§2. Logarithms
Many natural phenomena vary as a power function ax, so that they display exponential change over widely measurable ranges of the exponent x. Scientists are therefore often interested in the value of this exponent, which is called a logarithm.§2.1 Logarithms and Powers
Quite often when analyzing a power function y = ax , it is y that is the known quantity, and the exponent x is the value that one wishes to find.One then needs a function x = f(y) that is the inverse of the power function, which is called a logarithm:
y is called the argument of the logarithm.
Another way of saying this is that x is the exponent to which a must be raised to equal y:
x
|
=
| log a y |
if and only if
|
ax
|
=
| y | . |
Note that we can always very generally write:
y
|
=
| aloga y | , |
Examples:
x
|
=
| log 2 8 | ||
2x
|
=
| 8 = 23 | ||
x
|
=
| 3 | . |
4y
|
=
| 17 | ||
y
|
=
| log 4 17 | . |
Exercises:
Type 1: Find an expression for y given that x = log a y [substitute various symbols for {a, x, y}, as well as various symbols and simple numerical values for {a, x} — no ones or zeros].Type 2: Calculate x = log a y for {a, y} [substitute simple numerical values such as {2, 16}, {3, 27}, {1/9, 1/81}, etc. — no ones or zeros]
§2.2 Combinations of Logarithms
Some simple combinations of logarithms illustrate their utility.§2.2.1 Logarithms of Products
When the argument of a logarithm is a product of two numbers, log a (y · z), it can be split apart into the sum of two logarithms:
Explanation:
x
|
=
| log a (y · z) | ||
ax
|
=
| y · z | Why? | |
| = | aloga y · aloga z | Why? | ||
| = | aloga y + loga z | Why? | ||
x
| = | log a y + log a z | Why? . |
Examples:
x
|
=
| log 5 (2·3) | ||
| = | log 5 2 + log 5 3 | . |
x
|
=
| log a (y · z) | ||
ax
| = | y · z | Why? | |
y
| = |
ax/z
| . |
x
|
=
| aloga y + loga z | ||
| = | aloga y· aloga z | Why? | ||
| = |
y · z
| Why? . |
Exercises:
Type 1: Find an expression for x = log a (y · z) that involves logarithms of single arguments [substitute various symbols for {a, y, z}, as well as various simple numerical values for {a, y, z} — no ones or zeros].Type 2: Find an expression for y given that x = log a (y · z) [substitute various symbols for {a, y, z}].
Type 3: Find a more compact expression for x = log a y + log a z [substitute various symbols for {a, y, z}, as well as various simple numerical values for {a, y, z} — no ones or zeros].
Type 4: Find a more compact expression for x = aloga y + loga z that doesn't use any logarithms [substitute various symbols for {a, y, z}, as well as various simple numerical values for {a, y, z} — no ones or zeros].
§2.2.2 Logarithms of Quotients
When the argument of a logarithm is a quotient of two numbers, log a (y / z), it can also be split apart, into the difference of two logarithms:
Explanation:
x
|
=
| log a (y / z) | ||
ax
|
=
| y / z | Why? | |
| = | aloga y / aloga z | Why? | ||
| = | aloga y – loga z | Why? | ||
x
| = | log a y – log a z | Why? . |
Examples:
x
|
=
| log 5 (2/3) | ||
| = | log 5 2 – log 5 3 | . |
x
|
=
| log a (y/z) | ||
ax
| = | y/z | Why? | |
y
| = |
z · ax
| . |
x
|
=
| aloga y – loga z | ||
| = | aloga y/ aloga z | Why? | ||
| = |
y / z
| Why? . |
Exercises:
Type 1: Find an expression for x = log a (y / z) that involves logarithms of single arguments [substitute various symbols for {a, y, z}, as well as various simple numerical values for {a, y, z} — no ones or zeros].Type 2: Find an expression for x = log a (w · y / z) that involves logarithms of single arguments [substitute various symbols and simple numerical values for {a, w, y, z} — no ones or zeros].
Type 3: Find an expression for z given that x = log a (y / z) [substitute various symbols and simple numerical values for {a, y} — no ones or zeros].
Type 4: Find a more compact expression for x = aloga y – loga z that doesn't use any logarithms [substitute various symbols and simple numerical values for {a, y, z} — no ones or zeros].
§2.2.3 Logarithms of Power Functions
When the argument of a logarithm is a power of two numbers, log a by, it can also be split apart, into a multiple of a logarithm:
Explanation:
x
|
=
| log a by | |||
=
| log a (b·b·····b) | Why? | |||
y times
| |||||
| = | log a b + log a b+ ... + log a b | Why? | |||
y times
| |||||
| = | y log a b | . | |||
Example:
x
|
=
| log 5 8 | ||
=
| log 5 23 | |||
| = | 3 log 5 2 | . |
x
|
=
| log a (z · by) | ||
=
| log a z + log a by | Why? | ||
x – log a
|
z
| = | y log a b | |
y
| = |
(x – log a z)/log a b
| . |
x
|
=
| w log a y + log a z | ||
=
| log a yw + log a z | |||
| = | log a (yw · z) | Why? . |
x
|
=
| log a (by / bz) | ||
=
| log a by–z | Why? | ||
| = | (y – z) log a b | . |
Exercises:
Type 1: Find an expression for x = log a by that doesn't use any exponents [substitute various symbols for {a, b, y}, as well as various simple numerical values for {a, b, y} — no ones or zeros].Type 2: Find an expression for y given that x = log a (by · cz) [substitute various symbols for {a, b, c, y, z}, as well as various simple numerical values for {a, b, c, y, z} — no ones or zeros].
Type 3: Find an expression for x = v log a w + y log a z that involves only a single logarithm function [substitute various symbols for {a, v, w, y, z}, as well as various simple numerical values for {a, v, w, y, z} — no ones or zeros].
§2.3 Particular Argument Values
Some arguments of the logarithm function have special characteristics.§2.3.1 Special Arguments
Because any number raised to the power of 1 is equal to itself, a1 = a, the following identity will always be true for any argument equal to its base:Similarly, because any number raised to the power of 0 is equal to 1, a0 = 1, the following identity will always hold for any base a:
Because a power function ax only reaches a value of 0 for very large exponents x → – ∞ (a > 1) and x → + ∞ (a < 1), an argument of zero will result in:
Logarithms of negative arguments generally result in complex values, and their discussion is beyond the scope of this tutorial.
Examples:
x
|
=
| log 5 log 3 3 | ||
=
| log 5 1 | |||
| = | 0 | . |
x
|
=
| log a (ay / az) | ||
=
| log a ay – log a az | Why? | ||
| = | y log a a – z log a a | Why? | ||
| = |
y – z
| . |
x
|
=
| log 5 log 3 1 | ||
=
| log 5 0 | |||
| = | – ∞ | . |
Exercises:
Type 1: Calculate x = log b log a a [substitute various symbols for {a, b}, as well as various simple numerical values for {a, b} — no ones or zeros].Type 2: Calculate x = log b log a 1 [substitute various symbols for {a, b}, as well as various simple numerical values for {a, b} — no ones or zeros].
Type 3: Calculate x = log a (ay / az) [substitute various symbols for {a, b}, as well as various simple numerical values for {a, b} — no ones or zeros].
§2.4 Particular Base Values
Some values of the base of a logarithm have particular use and importance.§2.4.1 Common Logarithms
In science, large and small numbers are often expressed in scientific notation, e.g.
1,000,000
|
=
| 106 | , | |
| 3,512,000 |
=
| 3.512 x 106 | . |
x
|
=
| log 10 1,000,000 | ||
=
| 6 | . |
x
|
=
| log 10 3,512,000 | ||
=
| 6.5455545... |
The base-10 logarithm is called the common logarithm, and the subscript is typically dropped:
Exercises:
§2.4.2 Natural Logarithms
Another base that shows up naturally in calculus is the transcendental number e = 2.718281..., because the power of this base is equal to its own derivative.The base-e logarithm, the inverse of ex, is called the natural logarithm, and it is typically abbreviated ln:
This function can also be found on a scientific calculator (and again note that the ln key is usually implemented as inv ex, or vice-versa).
The exponential function can be used to define any other power function, because any base can be expressed as a power of e with a scaled exponent:
Explanation:
a
|
=
| eln a | Why? | |
ax
|
=
| (eln a)x | ||
=
| ex · ln a | Why? . |
Exercises:
§2.5 Graphs of Logarithm Functions
Since we have defined logarithm functions for all real positive arguments, we can draw graphs of them to see how they behave in general:
Note the special base a = 1, as well as the function values at the special arguments x = 1 and x = a.
Note also the up-down symmetry of log 2 x and log 0.5 x.
This graph should help you understand why logarithmic growth is commonly used to describe a slow increase.
http://webmath.amherst.edu/qcenter/logarithms/index.html
Subscribe to:
Comments (Atom)