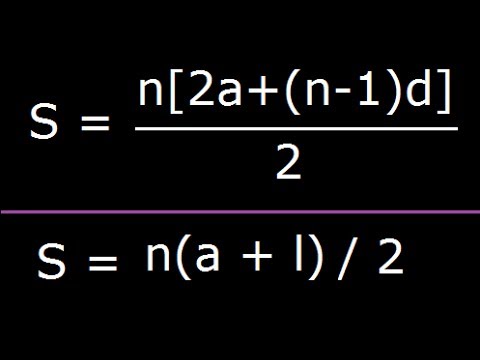UchihaMaths
Tuesday, 12 July 2016
Inequalities
| 1) | 
Graphically, the solution is:
| The only difference between the linear equation "x + 3 = 2" and this linear inequality is that I have a "less than" sign, instead of an "equals" sign. The solution method is exactly the same: subtract 3 from either side.Note that the solution to a "less than, but not equal to" inequality is graphed with a parentheses (or else an open dot) at the endpoint, indicating that the endpoint is not included within the solution. |
| 2) | 
Graphically, the solution is:
| The only difference between the linear equation "2 – x = 0" and this linear inequality is the "greater than" sign in place of an "equals" sign.Note that "x" in the solution does not "have" to be on the left. However, it is often easier to picture what the solution means with the variable on the left. Don't be afraid to rearrange things to suit your taste. |
| 3) | 
Graphically, the solution is:
| The only difference between the linear equation "4x + 6 = 3x – 5" and this inequality is the "less than or equal to" sign in place of a plain "equals" sign. The solution method is exactly the same.Note that the solution to a "less than or equal to" inequality is graphed with a square bracket (or else a closed dot) at the endpoint, indicating that the endpoint is included within the solution. |
| 4) |
Graphically, the solution is:
| The solution method here is to divide both sides by a positive two. Copyright © Elizabeth Stapel 1999-2011 All Rights Reserved |
| 5) | 
Graphically, the solution is:
| This is the special case noted above. When I divided by the negative two, I had to flip the inequality sign. |
http://www.purplemath.com/modules/ineqsolv.htm
this video will help u to understand more about the inequalities..

Arithmetic progression
Subscribe to:
Comments (Atom)